今天終於進入到了大家最喜歡的單元「三角函數」！

先暖個嗓子念一下咒語吧！

寐偲，摳賽！！！

進入正題吧～

這個我自己是在高中二年級上學期學到的，如果各位有印象的話就會知道 cos 就是一個角的餘弦值，對於一個直角三角形的角來說就是鄰邊 / 斜邊。

在圓上表示：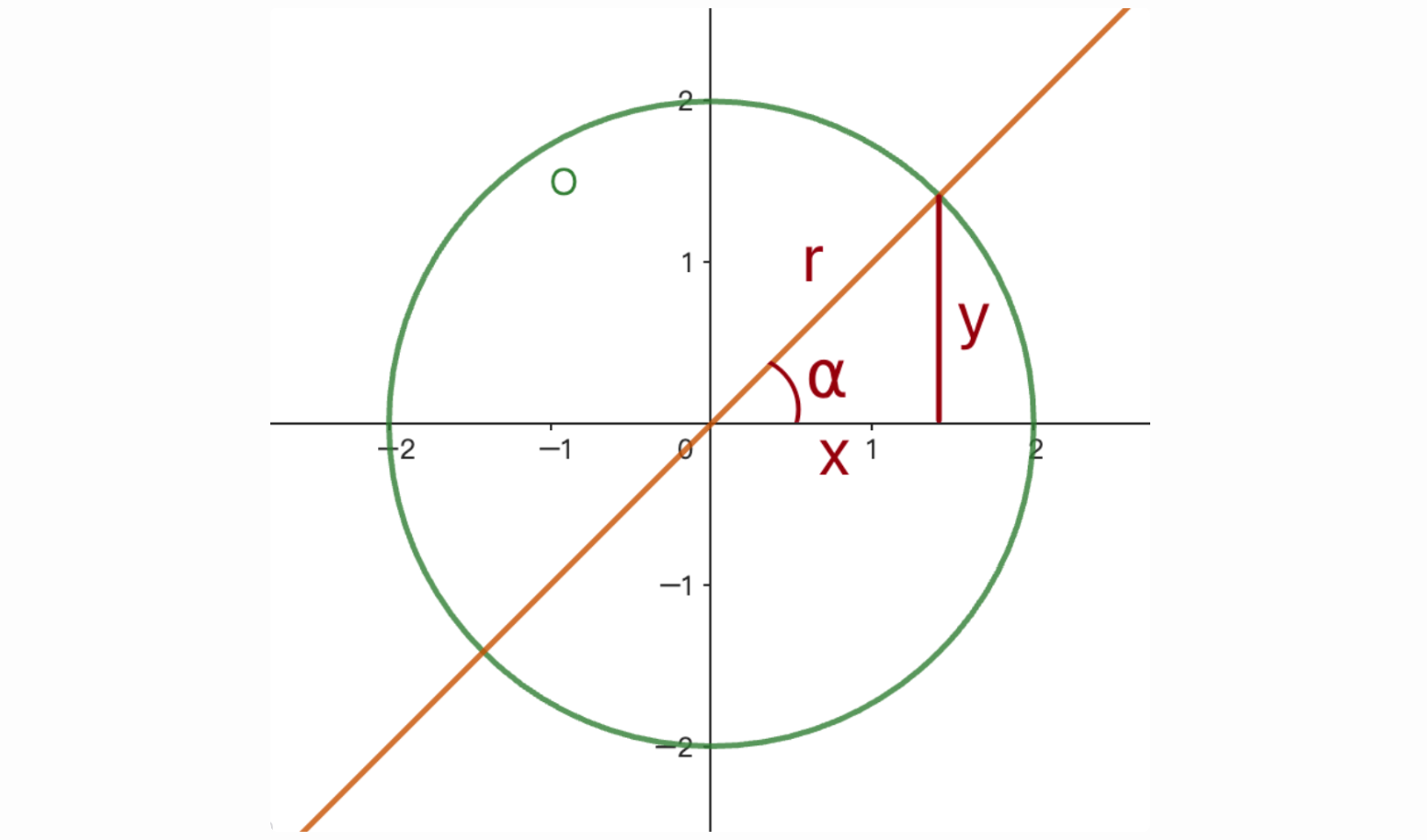

一個圓的半徑是r，圓心角是α，那 cosα 的值就會是x / r。

知道他的定義之後來看看Math.cos()怎麼使用吧！

語法

Math.cos(x)

參數

傳入一個以弧度表示的數值

回傳值

它會回傳x的cos（餘弦）值，介於-1到1之間（含）。
如果x是Infinity、-Infinity或NaN，則回傳NaN。

看看規範吧！

規範

函式回傳x的cos值，引數需要以角度表示。

步驟如下：

1. 令一個變數n，將ToNumber(x)賦值給n。
2. 如果n是無限大，回傳NaN。
3. 如果n是浮點數+0或浮點數-0，回傳浮點數1。
4. 他會回傳一個cos(R(n))的近似值。

關於近似值：

意思大概是針對某些計算的結果，規範沒有強制引擎計算的結果一定要完全正確，只要他們能夠足夠靠近真實的值就可以了。

所以我們可以來做點小測試，來看看這個方法有沒有符合我們預期。

根據我們的認知，cos的值在某些特定角度的值較好觀察：

• cos0°(cos0) = 1
• cos90°(cosπ/2) = 0
• cos180°(cosπ) = -1
• cos270°(cos3π/2) = -0

π代表著180°，JS提供了Math.PI來存放這個值（3.141592...）

那我們來帶進去看看：

Math.cos(0); //1
Math.cos(Math.PI / 2); //6.123233995736766e-17
Math.cos(Math.PI); //-1
Math.cos(Math.PI * 3 / 2); //-1.8369701987210297e-16

哪尼哪尼？尖尖哇嘎奈！！

cos90°的時候應該要為0，但是卻給出了6.123233995736766e-17
事實上他已經足夠接近0了，一直到小數點後第17位才有0以外的數字。

我們用一個Number.EPSILON（艾普西隆常數ε）來判斷這樣的誤差可不可以被接受吧！

const result = Math.cos(Math.PI / 2);
console.log(Math.abs(result - 0) < Number.EPSILON ? 0 : result); //0

結果回傳了0，表示Math.cos(Math.PI / 2)的值與實際cos(π/2)的值之誤差是可以被接受的！

應用

前面有提到cos的值會介於-1~1之間，讓我們來看一下y = cosx的圖形吧！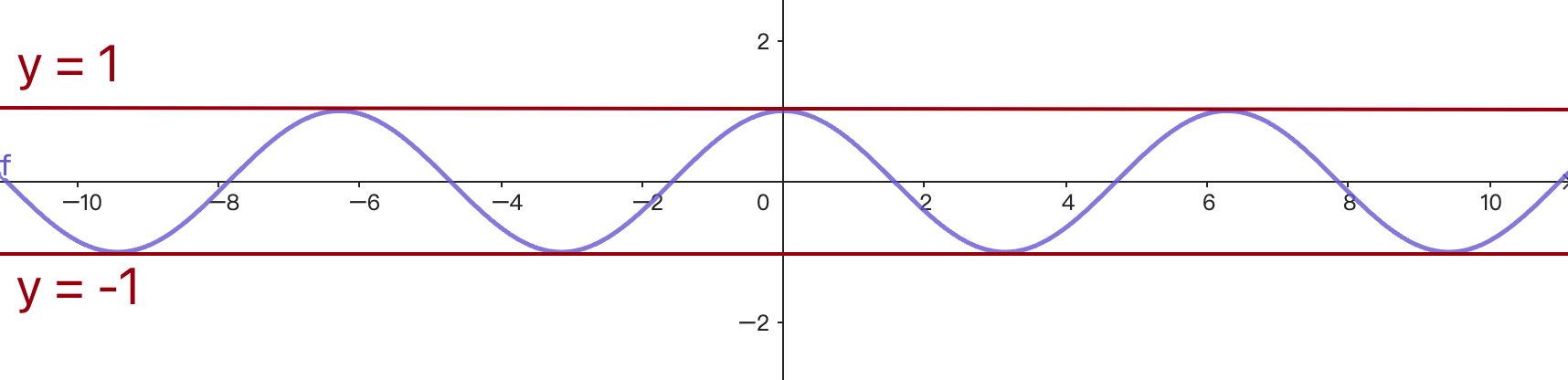

可以觀察到他是一個從-1到1不斷來回震盪的波浪圖，這個圖是不是也像極了心情正在坐雲霄飛車的各位呢？在靠近最高點（1）跟最低點（-1）時坡度減緩、速度變慢了（才不會撞到地板啊！咦？），所以可以想像他是一個不斷漸快漸慢的循環，將他套用在動畫是不是很有趣呢！！！

//html
<div class="block"></div>

//css
.block {
    position: absolute;
    top: 0;
    bottom: 0;
    left: 0;
    right: 0;
    margin: auto;
    width: 100px;
    height: 100px;
    background-color: brown;
}

//js
const block = document.querySelector(".block");
let scaleValue = 1;
let x = 0;
setInterval(() => {
    block.style.transform = `scale(${scaleValue})`;
    x++;
    scaleValue = Math.cos(x / 30) / 2 + 2;
}, 10);

很簡單建立一個block，用setInterval來將這個元素作不斷縮放，透過Math.cos()來控制數值會以漸變的方式增減，是不是很像東西在漂浮啊！

最後再試著唸唸看這個咒語吧！

寐斯，摳賽！！

哦哦！！！今天成功使出了漂浮特效咒語了！！明天見。

source code：
https://github.com/860824jeremy/Math/tree/main/Math_cos

參考資料：
MDN-Math.cos()
ECMAScript-Math.cos()